BIT Hacks - 자연수 승수 계산을 비트연산으로 빠르게 하는 법 - 단편글

자연수 승수 연산에 한해, 비트연산 트릭을 활용하여 C++에서 기본으로 제공하는 pow() 함수보다 빠르게 계산하는 방법을 알아봅니다.

TL;DR

 1double pow_int(double base, int exp)
 2{
 3    double result = 1.;
 4    while (exp)
 5    {
 6        if (exp & 1)
 7            result *= base;
 8        exp >>= 1;
 9        base *= base;
10    }
11    return result;
12}

01_result

원리

실수 $$a$$ 와 자연수 $$n$$ 에 대하여, $$a^n$$ 을 계산하는 경우를 살펴보겠습니다.

여기서 $$n$$ 은 2진법 변환을 통해 다음과 같이 표현할 수 있습니다.

n = \sum_{i=0} b_i 2^i \text{, where }b_i=0 \text{ or }1

위 식을 이용하면 $$a^n$$ 은 다음과 같이 변형됩니다.

\begin{aligned} a^n & = a^{\sum_{i=0} b_i 2^i} \\\\ & = \prod_{i=0} {a^{b_i 2^i}} \text{ (} \because x^{m+n} = x^m x^n \text{)} \\\\ & = \prod_{i=0} ({a^{2^i}})^{b_i} \text{ (} \because x^{mn} = (x^m)^n \text{)} \\\\ & = (b_0 \times a) \times (b_1 \times a^2) \times (b_2 \times (a^2)^2) \times (b_3 \times ((a^2)^2)^2) \times ... \end{aligned}

이 식의 의미를 해석해보면 다음과 같습니다.

$$n$$ 을 2진법으로 나타내었을 때 낮은 자리수부터 확인( $$b_0, b_1, ...$$ )
매 $$b_i$$ 를 확인할 때마다, $$a, a^2, (a^2)^2, ...$$ 의 형태로 계속 제곱해 나감
$$b_i$$ 가 $$0$$ 이면 그냥 넘어가고,

$$b_i$$ 가 $$1$$ 이면 2에서 구한 $a^{2^i}$ 를 누적하여 곱함

예시

$$3^5$$ 를 계산해보겠습니다. 여기서 $$a=3$$ 이고, $$n=5$$ 가 됩니다.

먼저, $$n$$ 을 2진법으로 변환하여 $$b_i$$ 들을 구합니다.
$n=5=1+4=1\times2^0+0\times2^1+1\times2^2$ $\text{i.e. }b_0=1 \text{, } b_1=0 \text{, } b_2 = 1 \text{, and } b_k = 0 \text{ for }k>=3$
이제 낮은 자리 수부터 확인하며 누적곱 작업을 수행합니다.
1. 누적곱의 초기 값은 곱셈의 항등원인 1로 설정합니다.
2. $$a$$ 는 3입니다.
  
  $$b_0$$ 을 확인합니다. $$b_0$$ 가 $$1$$ 이므로, 1에 3을 곱합니다.
  
  결과는 3이 됩니다.
3. $$a^2$$ 는 9입니다.
  
  $$b_1$$ 을 확인합니다. $$b_1$$ 가 $$0$$ 이므로, 아무것도 곱하지 않습니다.
  
  결과는 여전히 3입니다.
4. $$(a^2)^2$$ 는 81입니다.
  
  $$b_2$$ 을 확인합니다. $$b_2$$ 가 $$1$$ 이므로, 3에 81을 곱합니다.
  
  결과는 243이 됩니다.
5. 이후의 $$b_k$$ 들은 모두 $$0$$ 이므로 이후에는 아무것도 곱하지 않습니다.
6. 따라서 최종 결과는 243입니다.

코드로의 적용(C++)

위 내용을 코드로 변환하면 다음과 같습니다.

변수명의 의미를 고려하여, 위 식에서 $$a$$ 를 base로, $$n$$ 을 exp로 명명하였습니다.

 1double pow_int(double base, int exp)
 2{
 3    double result = 1.;
 4    while (exp)
 5    {
 6        if (exp & 1)
 7            result *= base;
 8        exp >>= 1;
 9        base *= base;
10    }
11    return result;
12}

누적곱을 수행하기 위한 result 변수의 초기 값을 곱셈의 항등원인 1로 설정합니다.
exp 값이 유효한 동안 while 반복문을 수행합니다.
1. exp를 2진법으로 표현하였을 때 의 가장 낮은 자리수를 구합니다. (exp & 1)
  
  만약 이 값이 1이라면, $$b_i$$ 가 1인 경우에 해당합니다. 따라서, 현재의 base 값을 result에 누적하여 곱합니다.
  
  만약 이 값이 0이라면, $$b_i$$ 가 0인 경우에 해당합니다. 따라서 result에 아무것도 곱하지 않고 넘어갑니다.
  
  예를 들어, exp의 $$b_0$$ 값이 1이었다면, while 반복문을 맨 처음 수행할 때 이 if 조건이 참이 되어, result *= base; 구문이 수행되고, 위 설명에서 $a$를 곱해주는 것과 동일한 작업이 이루어집니다.
2. exp를 오른쪽으로 한 칸 비트시프트를 수행합니다. (exp >>= 1;)
  
  이를 통해, 방금 살펴본 $$b_i$$ 가 버려지고, 그 다음 자리에 해당하는 $b_{i+1}$ 이 가장 낮은 자리로 옮겨지는 과정이 반복됩니다.
3. base를 제곱합니다. (base *= base;)
  
  이를 통해 $$(...(a^2)^2)...)^2$$ 에 해당하는 반복 연산이 수행됩니다.
최종적으로 누적곱이 수행된 결과를 반환합니다. (return result;)

pow() 함수와의 비교용 예시 코드

코드

 1#include <iostream>
 2
 3double pow_int(double base, int exp)
 4{
 5    double result = 1.;
 6    while (exp)
 7    {
 8        if (exp & 1)
 9            result *= base;
10        exp >>= 1;
11        base *= base;
12    }
13    return result;
14}
15
16int main()
17{
18    const int N = 100000000;
19    double base = 12.345;
20    int exp = 67;
21    double result1, result2;
22
23    std::cout << base << "^" << exp << "\n\n";
24
25    auto startT1 = clock();
26    for (int i = 0; i < N; ++i)
27        result1 = pow(base, exp);
28    auto endT1 = clock();
29    std::cout << "Calculated by pow() function\n";
30    std::cout << "Answer: " << result1 << "\n";
31    std::cout << "Elapsed time: " << (endT1 - startT1) << " ms\n\n";
32    
33    auto startT2 = clock();
34    for (int i = 0; i < N; ++i)
35        result2 = pow_int(base, exp);
36    auto endT2 = clock();
37    std::cout << "Calculated by pow_int() function\n";
38    std::cout << "Answer: " << result2 << "\n";
39    std::cout << "Elapsed time: " << (endT2 - startT2) << " ms\n\n";
40
41    return 0;
42}

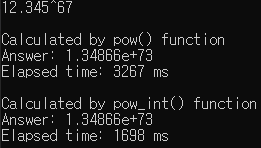
결과

i5-9500 @ 3.00GHz 기준

01_result