Geant4 무작정 따라하기 - 3. 다양한 모양의 지오메트리 만들기
Geant4 무작정 따라하기 시리즈의 세번째. 다양한 모양의 지오메트리를 만들기 위해 Solid에 대해 살펴봅시다.
Geant4에서는 다양한 종류의 Solid(형태)를 제공하고 있습니다. 이번 글에서는 다양한 Solid들을 사용해보도록 하겠습니다.
Geant4에서의 단위
Solid를 알아보기에 앞서, 단위라는 개념부터 살펴보려 합니다. Solid를 만들 때 크기를 입력하려면 길이에 대한 단위가 필수적으로 요구되기 때문입니다.
Geant4에서는 각종 물리량에 대한 단위를 제공하고 있으며, 이를 사용하기 위해서는 “G4SystemOfUnits.hh” 헤더가 필요합니다. 현재 작업 중인 DetectorConsturction.cc 파일에는 제가 이미 이 헤더를 추가해 놓았으므로, 바로 사용할 수 있습니다.
사용은 실제 물리량을 기술할 때와 동일한 방식으로 사용하면 됩니다만, 곱하기를 명시해주어야 한다는 점만 주의하면 됩니다.
예를 들어, 10 cm 라는 길이를 Geant4 코드 작성에서 기술하고자 할 때에는 다음과 같이 입력합니다.
110. * cm
길이 단위 이외에도, 질량, 밀도, 온도, 기압, 흡수선량 등 다양한 물리량에 대한 단위를 제공하고 있으므로, 필요에 따라 활용해보시기 바랍니다.
Solid의 여러가지 종류
Solid는 간단히 말해 입체도형입니다. 입체도형에는 직육면체, 원기둥, 구, 원뿔 등 다양한 모양이 있지요. Geant4에서도 Solid라는 개념 아래에 하위 개념으로서 G4Box(직육면체), GTubs(원기둥), G4Orb/G4Sphere(구), G4Cons(원뿔) 등을 만들어, 다양한 모양을 정의할 수 있게 하였습니다.
우리는 Geant4에서 어떤 입체도형을 제공하는지 파악하고, 각각의 입체도형을 정의하는 방법을 학습한 뒤, 그대로 사용하기만 하면 됩니다.
Geant4에서 제공하고 있는 Solid의 모든 종류는 Geant4 Doxygen에서 G4VSolid 클래스의 레퍼런스 페이지(10.7.p01 버전)에 들어가면 상속받은 클래스 목록(Inheritance diagram for G4VSolid) 부분을 통해 확인할 수 있습니다. 그 종류가 너무나도 많기 때문에, 이 글에서는 다음 세 가지 클래스의 생성자만 살펴보겠습니다.
- G4Box
- G4Tubs
- G4Orb
G4Box(직육면체)
G4Box는 직육면체 모양을 정의하는 데에 사용하는 클래스입니다. 클래스의 생성자는 다음과 같습니다.
1G4Box (const G4String &pName,
2 G4double pX,
3 G4double pY,
4 G4double pZ);
- pName: 정의할 직육면체의 이름. 자유롭게 적으면 됨
- pX: X축 방향으로의 모서리 길이의 절반
- pY: Y축 방향으로의 모서리 길이의 절반
- pZ: Z축 방향으로의 모서리 길이의 절반
간단히 말해, 직육면체를 정의하기 위해 필요한 것은, 이름과 가로, 세로, 높이라고 볼 수 있습니다. 다만, 가로, 세로, 높이의 경우에는 그 길이의 절반을 입력해야 한다는 점에 주의하세요.
예를 들어, X축 방향으로 10 cm, Y축 방향으로 5 cm, Z축 방향으로 20 cm 크기를 가진 직육면체 형태의 팬텀을 정의하고자 한다면 다음과 같이 입력하면 됩니다.
1auto phantomSol = new G4Box("phantom", 5. * cm, 2.5 * cm, 10. * cm);
다만, 이렇게 적으면 실제 직육면체 크기와 코드에 써있는 값이 서로 달라 헷갈리는 경우가 있어, 저는 개인적으로 다음과 같이 실제 길이에 0.5를 곱하는 형태로 적는 것을 선호합니다.
1auto phantomSol = new G4Box("phantom", .5 * 10. * cm, .5 * 5. * cm, .5 * 20. * cm);
각 변의 길이를 변수화한다면 다음과 같이 좀 더 알아보기 쉽게 적을 수 있겠지요.
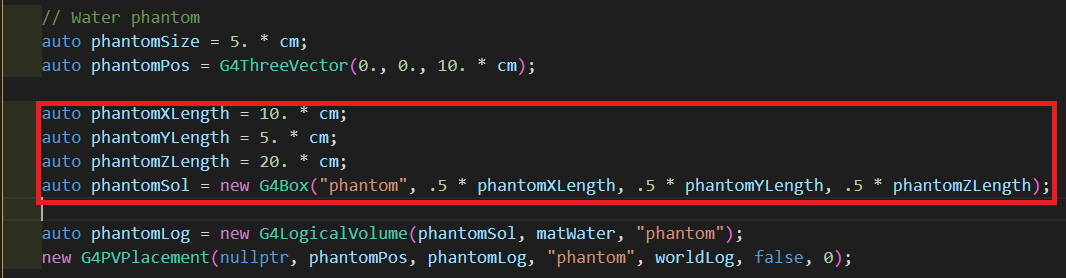
1auto phantomXLength = 10. * cm;
2auto phantomYLength = 5. * cm;
3auto phantomZLength = 20. * cm;
4auto phantomSol = new G4Box("phantom", .5 * phantomXLength, .5 * phantomYLength, .5 * phantomZLength);
지난 글에서 작성한 코드 부분 중, Solid에 해당하는 내용을 위 코드로 바꿔준 모습입니다.
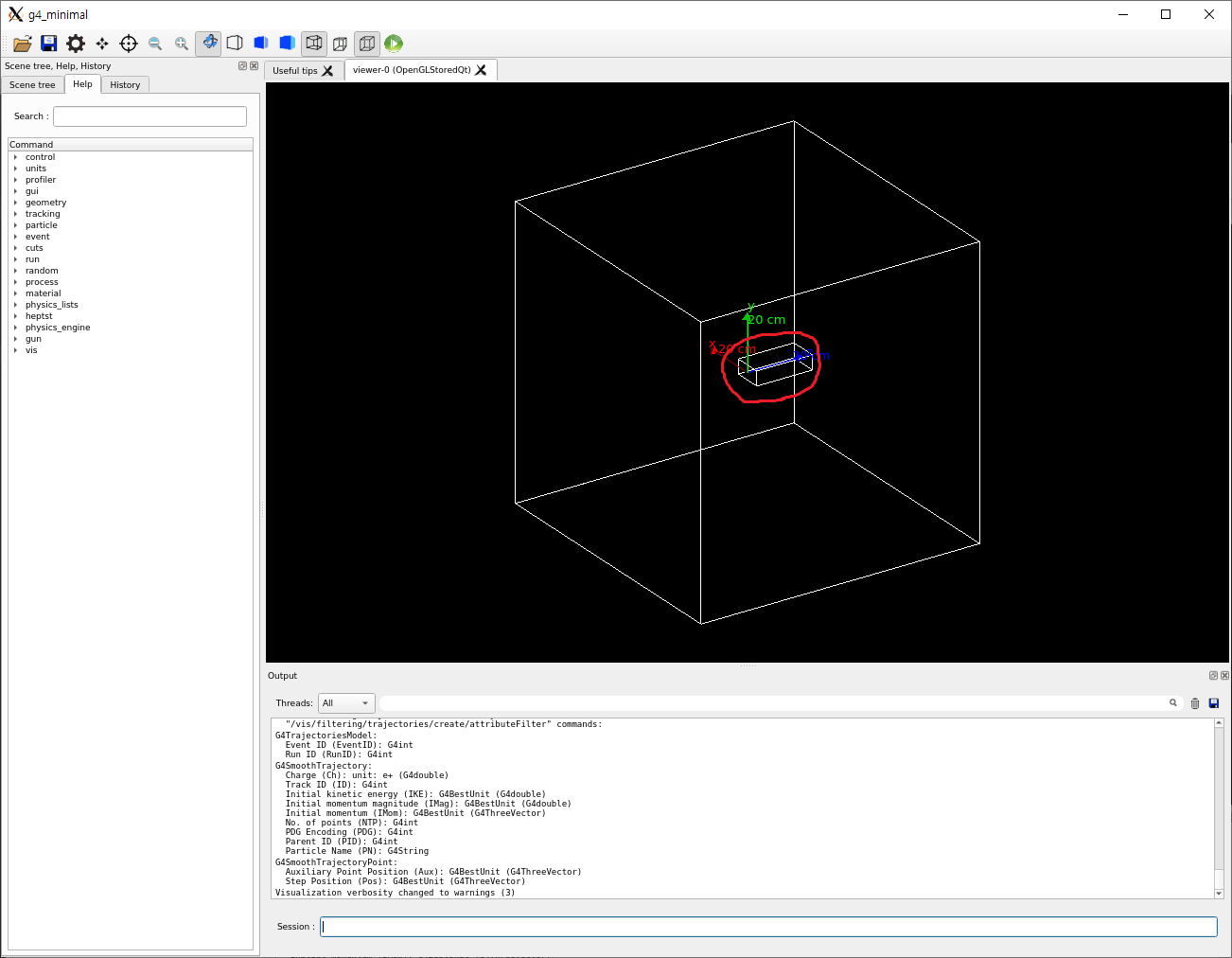
이 상태로 실행해보면, 물팬텀의 크기가 바뀐 것을 확인할 수 있습니다.
G4Tubs(원기둥)
G4Tubs는 원기둥 모양을 정의하는 데에 사용하는 클래스입니다. 가운데가 빈 두루마리 휴지같은 모양도 표현할 수 있습니다. 클래스의 생성자는 다음과 같습니다.
1G4Tubs (const G4String &pName,
2 G4double pRMin,
3 G4double pRMax,
4 G4double pDz,
5 G4double pSPhi,
6 G4double pDPhi);
-
pName: 정의할 원기둥의 이름. 자유롭게 적으면 됨
-
pRMin: 내반경. 속이 꽉 찬 원기둥이라면 0을 적고, 가운데가 빈 원기둥이라면 내부 원의 반지름을 적음
-
pRMax: 외반경. 외부 원의 반지름을 적음
-
pDz: 원기둥 높이의 절반
-
pSPhi: 시작 중심각. 케이크 조각처럼 부채꼴 기둥을 표현하고자 하는 경우에, 시작할 각도를 0°~360° 사이에서 지정할 수 있음. 일반적인 원기둥의 경우 0을 적음. (0°: +x축, 90°: +y축)
-
pDPhi: 중심각의 변화량. 케이크 조각처럼 부채꼴 기둥을 표현하고자 하는 경우에, 중심각의 변화량을 0°~360° 사이에서 지정할 수 있음. 일반적인 원기둥의 경우 360°(360. * deg)를 적음
일반적인 원기둥 뿐만 아니라, 원기둥 껍질 혹은 부채꼴 기둥 및 부채꼴 기둥 껍질모양까지 만들 수 있습니다.
예를 들어, 반지름이 5 cm이고, 높이가 10 cm인 속이 꽉 찬 원기둥 형태의 팬텀을 정의하고자 한다면 다음과 같이 입력하면 됩니다.
1auto phantomSol = new G4Tubs("phantom", 0., 5. * cm, 5. * cm, 0., 360. * deg);
저는 G4Box의 경우와 유사하게, 반경대신 직경을 써서 코드 작성시의 일관성을 유지하는 것을 좋아합니다. 일반적으로 다음과 같이 작성하는 편이지요.
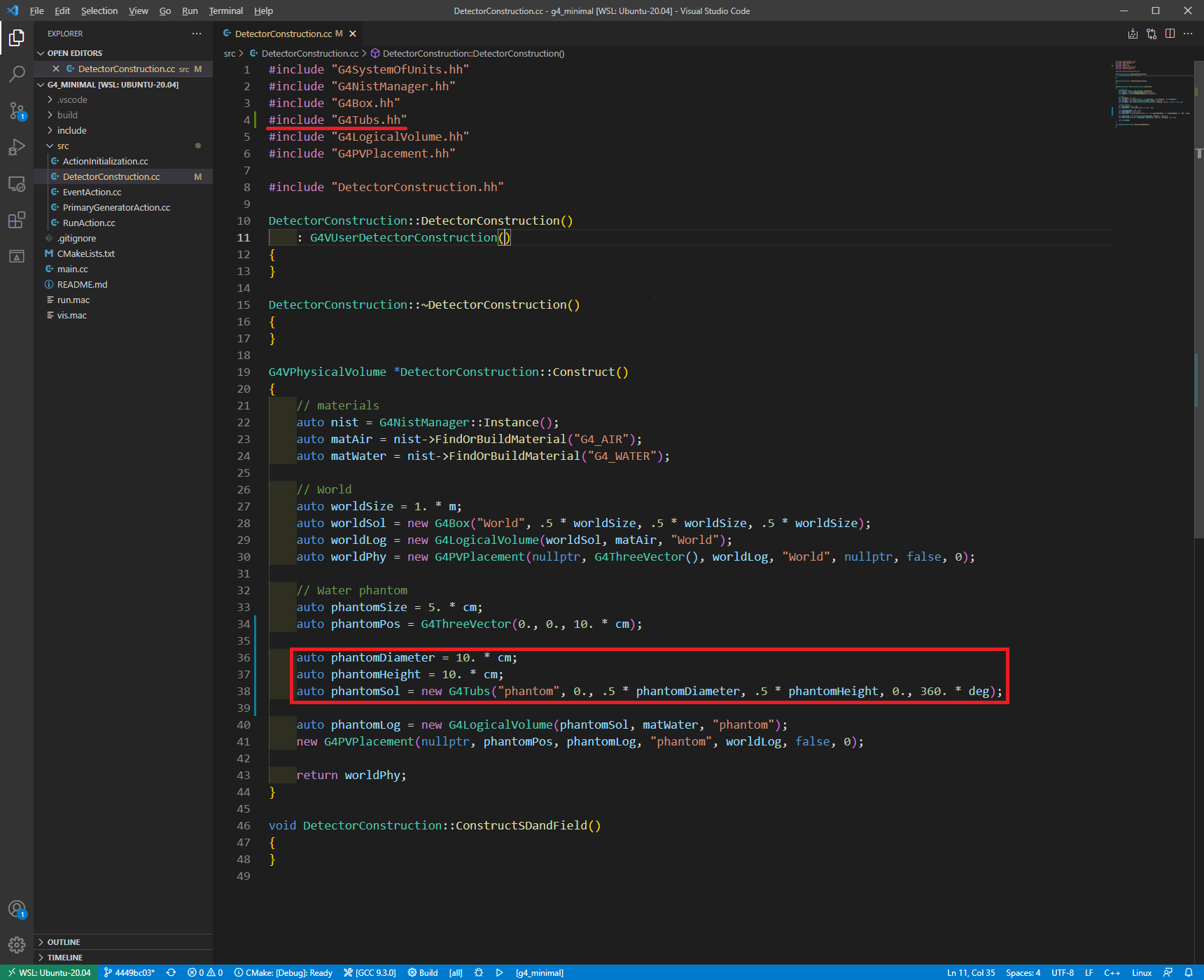
1auto phantomDiameter = 10. * cm;
2auto phantomHeight = 10. * cm;
3auto phantomSol = new G4Tubs("phantom", 0., .5 * phantomDiameter, .5 * phantomHeight, 0., 360. * deg);
아까 수정하였던 Solid에 해당하는 내용을 G4Tubs의 예시인 위 코드로 바꿔준 모습입니다. G4Tubs의 헤더(G4Tubs.hh)는 제가 제공해드렸던 템플릿 코드의 DetectorConstruction에 기본으로 포함되어 있지 않으므로, 꼭 직접 넣어주셔야 합니다.
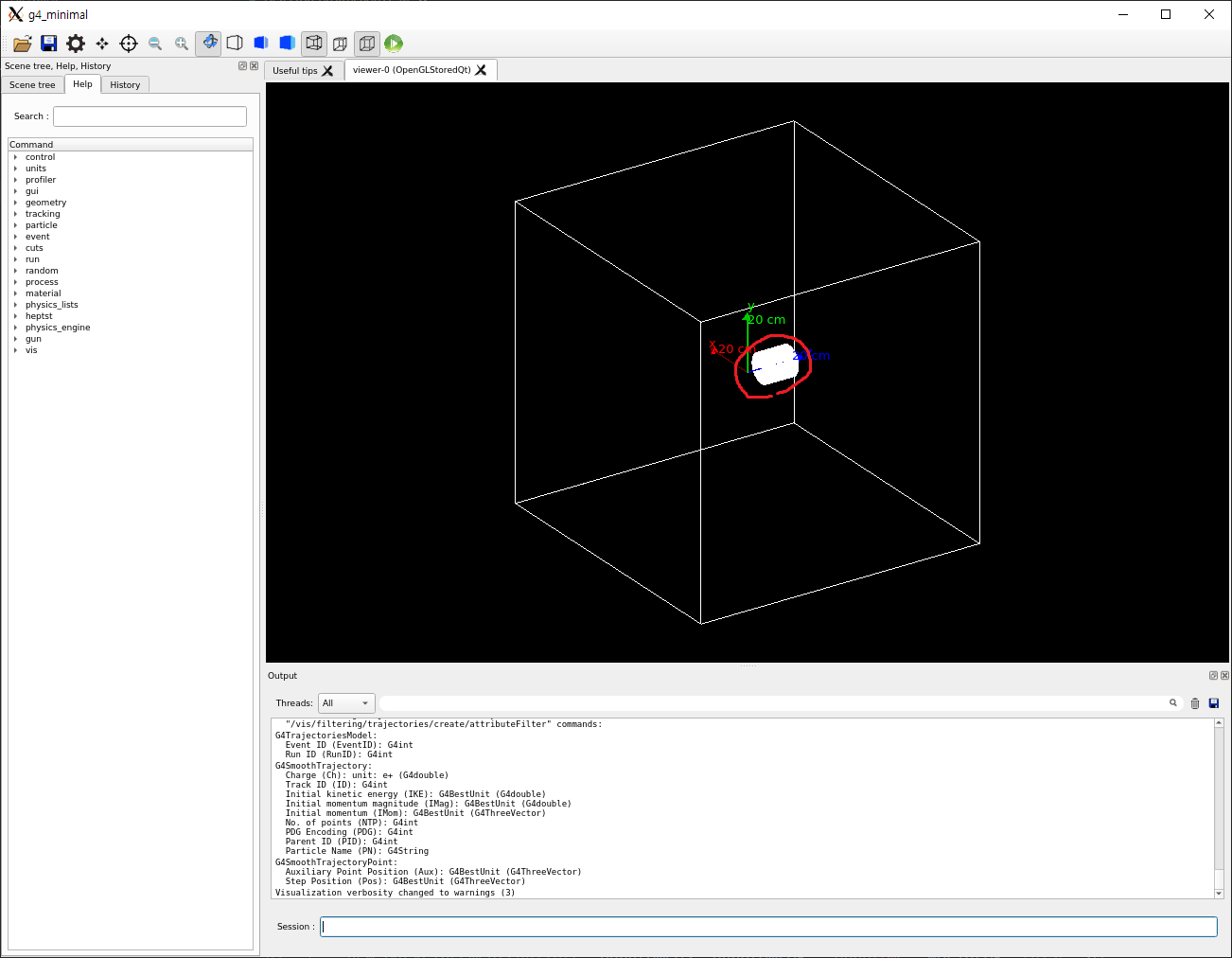
실행해보면, 물팬텀의 모양이 바뀐 것을 확인할 수 있습니다.
G4Orb(구)
G4Orb는 구 모양을 정의하는 데에 사용하는 클래스입니다. 클래스의 생성자는 다음과 같습니다.
1G4Orb (const G4String &pName,
2 G4double pRmax);
- pName: 정의할 구의 이름. 자유롭게 적으면 됨
- pRmax: 구의 반지름
G4Orb는 속이 꽉 찬 구만 만들 수 있습니다. 단순히 구의 반지름만 적어주면 끝이죠.
예를 들어, 반지름이 5 cm인 구형 팬텀을 정의하고자 한다면 다음과 같이 입력하면 됩니다.
1auto phantomSol = new G4Orb("phantom", 5. * cm);
저는 여기서도 직경을 이용하는 편입니다.
1auto phantomDiameter = 10. * cm;
2auto phantomSol = new G4Orb("phantom", .5 * phantomDiameter);
아까 수정하였던 Solid에 해당하는 내용을 G4Orb의 예시인 위 코드로 바꿔준 모습입니다. 이 경우에도 반드시 G4Orb의 헤더(G4Orb.hh)를 직접 넣어주시기 바랍니다.
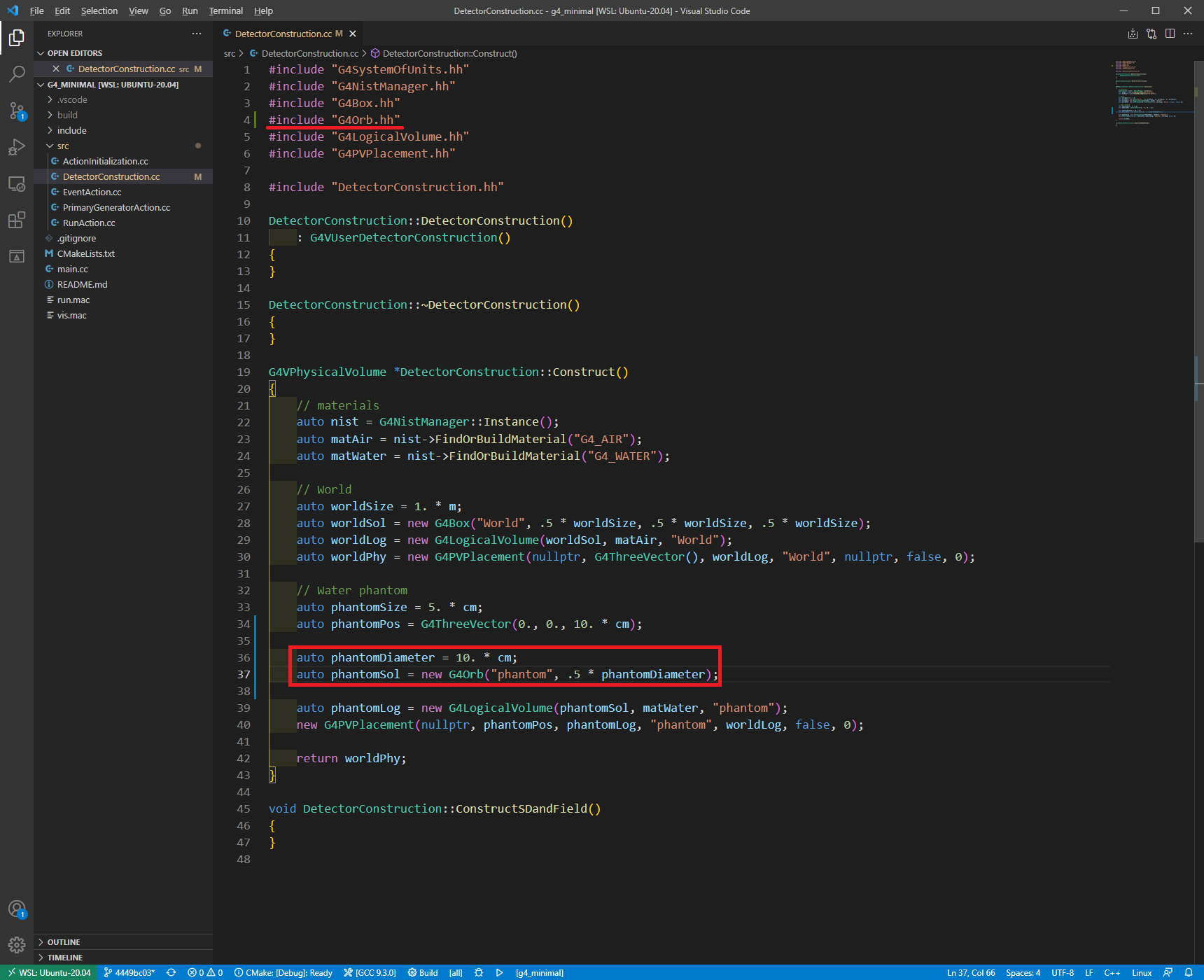
실행하면, 구형의 물팬텀을 확인할 수 있습니다.
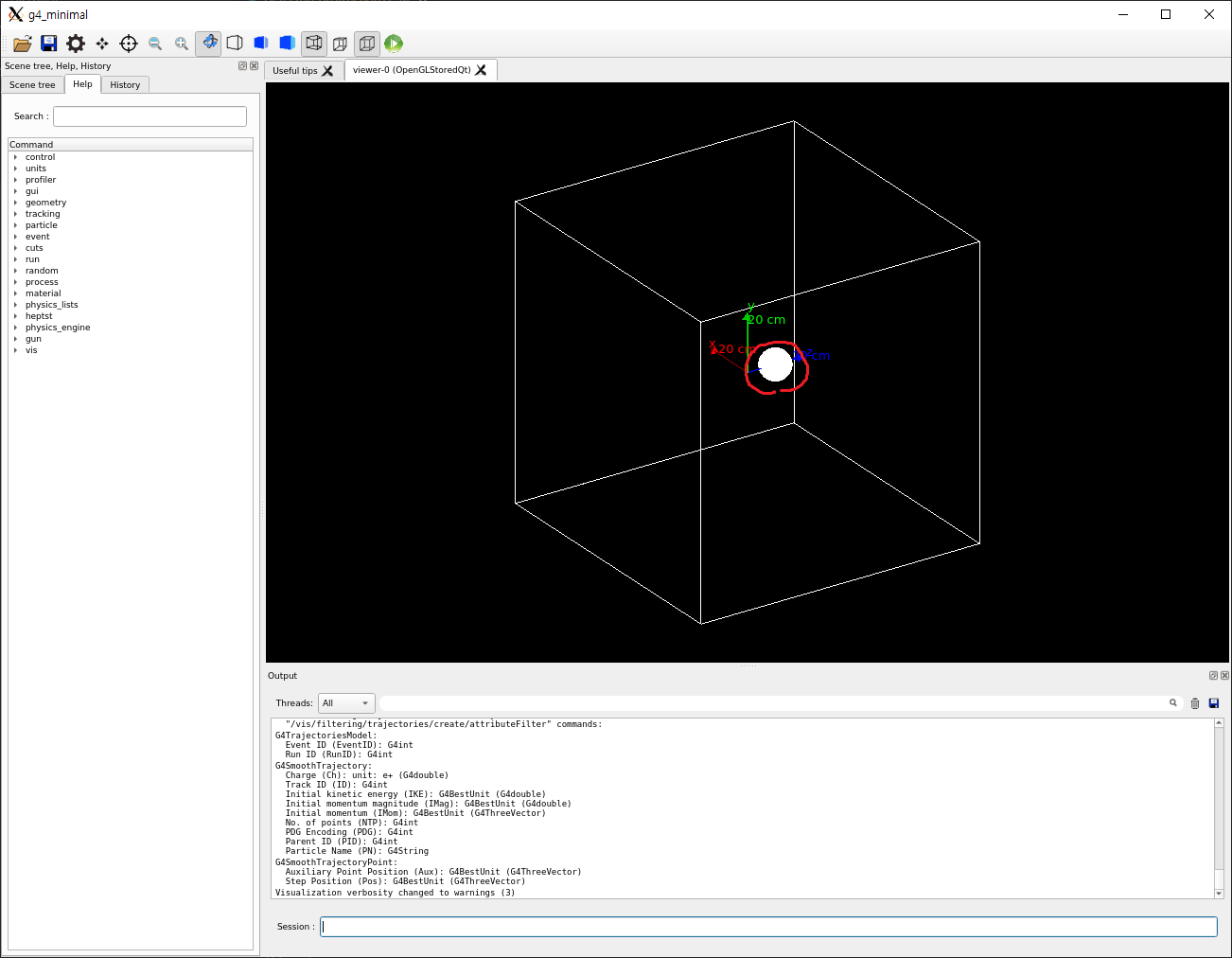
정리
Geant4는 이 외에도 정말 많은 Solid 종류를 제공하고 있습니다. 대부분의 경우, 각 클래스의 헤더파일을 열어보면 어떤 모양을 어떤 변수로 표현하는지 주석으로 설명되어 있습니다.
이 글에서 소개한 단순한 모양 이외에도, 두 개의 Solid를 이용하여 합집합/차집합/교집합에 해당하는 새로운 Solid를 정의하는 클래스 (G4UnionSolid, G4SubtractionSolid, G4IntersectionSolid)나, 다각형 면으로 구성된 지오메트리를 표현하기 위한 Solid 클래스 (G4TesellatedSolid) 등 다양한 클래스를 제공하고 있으니 필요에 따라 참고하시기 바랍니다.
고생하셨습니다.
다음 글에서는, 물질을 정의하는 방법에 대해 좀 더 자세히 살펴보도록 하겠습니다.